Introduction to (Big O Notation)

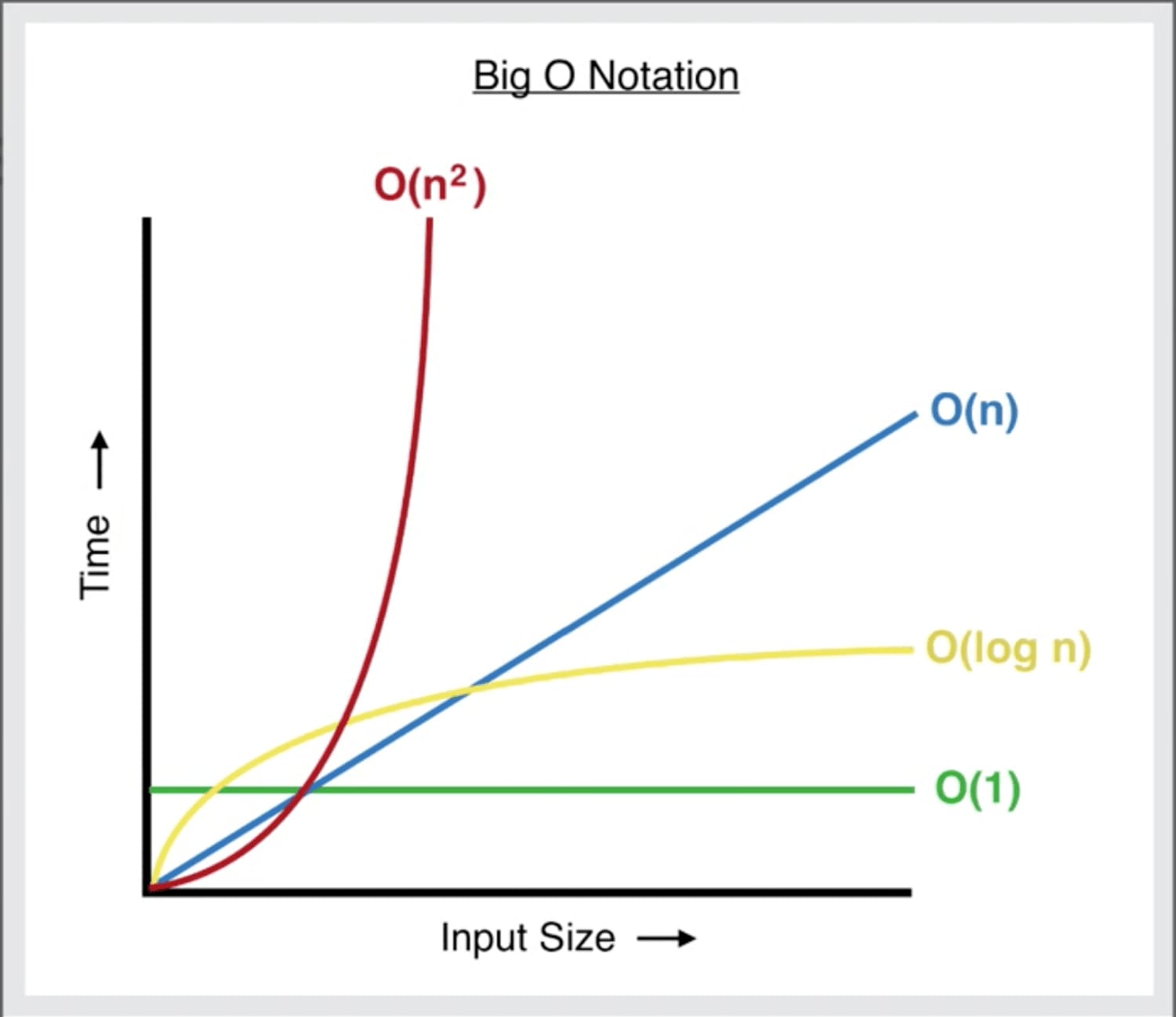
কম্পিউটার সাইন্সে কোনো একটা অ্যালগরিদমের পারফরমেন্স(performance) বা কমপ্লিক্সিটি(complexity) কে বোঝাতে বিগ ও নোটেশন (Big O) ব্যাবহার করা হয়। বিগ ও নোটেশন (Big O) স্পেশালি(specifically) অ্যালগরিদমের টাইম বা স্পেস কমপ্লিক্সিটির(complexity) ওয়ার্স্ট-কেস(worst-case) কে নির্দেশ করে।

ওয়ার্স্ট-কেস(worst-case) কি?

[1,2,3,4,5,6]

ধরি, আমাদের কাছে উপরোক্ত অ্যারেটি আছে । এবং আমরা দেখতে পাইতেছি যে, অ্যারের সর্বশেষ আইটেমটি হলো 6 । এখন আমাদেরকে যদি কোনো একটা অ্যালগরিদম ব্যাবহার করে 6 কে খুজতে বলা হয় তাহলে কিন্তু অন্য আইটেম গুলোর থেকে অপারেশন বেশি করতে হবে এবং সময়ও বেশি লাগবে, আর এটিই এই অ্যালগরিদমের ওয়ার্স্ট-কেস(worst-case)। অনেকেই ওয়ার্স্ট-কেস(worst-case) কে খারাপ কেসও বলে থাকে ।

প্রোগ্রামার যখন কোনো একটা অ্যালগরিদম লিখে তখন অবশ্যই তাকে পারফরমেন্স(performance) বা কমপ্লিক্সিটি(complexity) এর কথা মাথায় রেখে লিখতে হয়। একটা অ্যালগরিদম তো অনেক ভাবেই লিখা যায় কিন্তু কোন অ্যালগরিদমটি ব্যাবহার করলে মেমরি এবং সময় কম নিবে তা আগে বুঝতে হবে । তবে একটা কথা বলে রাখা ভালো যে, অনেক সময় একটি অ্যালগরিদমের মেমরি বাঁচাতে অতিরিক্ত সময় খরচ করতে হয়, আবার সময় বাঁচাতে অতিরিক্ত মেমরি খরচ করতে হয় ।

কোনো একটি অ্যালগরিদম রান করতে কি পরিমাণ সময় নিবে বা অ্যালগরিদমটি কি পরিমাণ মেমরি নিবে এগুলোর হিসেব-নিকেশ বিগ ও নোটেশন (Big O) এর দ্বারা করা হয়।

বিগ ও নোটেশন (Big O) ছাড়াও আরও দুইটি গাণিতিক ফাংশন আছে ।

১। থেটা(Θ)

এটি মূলত অ্যালগরিদমের এভারেজ কেস হিসেব করতে ব্যাবহার করা হয়।

২। ওমেগা(Ω)

এটি মূলত অ্যালগরিদমের বেস্ট কেস হিসেব করতে ব্যাবহার করা হয়।

এই ব্লগে আমরা শুধু ডেফিনেশন দিয়ে বুঝবো যে টাইম এবং স্পেস কমপ্লিক্সিটি(complexity) কি ? এবং পরের ব্লগে স্পেসেফিকভাবে টাইম এবং স্পেস কমপ্লিক্সিটি(complexity) নিয়ে বিস্তর আলোচনা করার চেষ্টা করবো ।

- টাইম কমপ্লিক্সিটি(complexity) -

অ্যালগরিদম বা প্রোগ্রামে টাইম কমপ্লিক্সিটি(complexity) অনেক গুরুত্বপূর্ণ বিষয় । সোজা-সাপ্টায় কোনো অ্যালগরিদম বা প্রোগ্রাম রান হতে কতটুকু সময় লাগলো তাকেই টাইম কমপ্লিক্সিটি(complexity) বলে। কোনো একটা প্রোগ্রাম রান হতে ঠিক কতটুকু সময় নিলো তা আমরা বিভিন্ন লাইব্রেরী ফাংশনের সাহায্যে বের করতে পারি । কিন্তু যদি আমরা একবার এর হিসেব-নিকেশ বুঝি তাহলে যেকোনো প্রোগ্রাম রান না করেই অর্থাৎ দেখলেই বলে দিতে পারবো যে সেই প্রোগ্রাম রান হতে কেমন সময় লাগতে পারে ।

- টাইম কমপ্লিক্সিটি(complexity) মাথায় রাখা কেনো দরকার-

বিভিন্ন অনলাইন জাজে কোনো একটা পব্লেম পড়ার সময় দেখবেন যে, উপরে বা কোথাও টাইম লিমিট মেনশন করা থাকে । যার অর্থ হইলো যে, আপনি যেভাবেই প্রোগ্রামটা লিখেন নাহ কেনো প্রোগ্রাম রান হতে মেনশন করা সময়ের বেশি যেনো নাহ লাগে।

এছাড়াও, ইউজার এক্সপেরিয়েন্সের জন্য টাইম কমপ্লিক্সিটি(complexity) একটা প্রধান বিষয় । এখন আপনি একটি অ্যাপ্লিকেশন তৈরি করলেন দেখা গেলো যে, সেটির কোনো একটা পার্টে ইউ-আই বা ডাটা লোড হতে নির্দিষ্ট সময়ের থেকে অনেক বেশি সময় লাগতেছে । এখন আপনার কি মনে হয় যে ইউজার এটি ব্যাবহার করবে? অবশ্যই নাহ করার সম্ভাবনাটা বেশিই ।

- স্পেস কমপ্লিক্সিটি(complexity) -

অবশ্যই অ্যালগরিদম বা প্রোগ্রামে স্পেস কমপ্লিক্সিটি(complexity)ও গুরুত্বপূর্ণ বিষয় । একটি অ্যালগরিদম বা প্রোগ্রাম সম্পন্ন করার জন্য ঠিক কতটুকু জায়গা বা মেমরি নিলো তাকেই স্পেস কমপ্লিক্সিটি(complexity) বলে।

কোনো অ্যালগরিদম বা প্রোগ্রামের জন্য আমাদের নির্দিষ্ট মেমরি ব্যাবহার করতে হয়। কিন্তু আমরা যদি স্পেস কমপ্লিক্সিটির(complexity) হিসেব-নিকেশ বুঝি তাহলে সহজেই বলে দিতে পারবো যে একটি প্রোগ্রাম কার্যকর করার জন্য ঠিক কতটুকু মেমরি ব্যাবহার করতে হবে।

- Common orders in Big (O) -

আগেই বলেছি যে, কোনো একটা সমস্যা অনেকভাবে অ্যালগরিদম বা প্রোগ্রাম লিখে সমাধান করা যায় । আর এখানেই আসে ওর্ডার অপারেশন অর্থাৎ সমস্যাটি সমাধান করার আগে জানতে হবে যে, কোন অ্যালগরিদমের কমপ্লিক্সিটি(complexity) কত ? কম না বেশি । অবশ্যই একটি সমস্যা সমাধান করতে সবচেয়ে কম সময় বা মেমরি যাতে লাগে এরকম একটা অ্যালগরিদম লিখার চেষ্টা করতে হবে।

আর এসব বুঝতে কিছু ওর্ডার অপারেশন সমন্ধে জানতে হবে যেমন -

• O(1)
• O(n)
• O(!n)
• O(n2)
• O(n3)
• O(log n)

ইত্যাদি ইত্যাদি । এগুলো কে ওর্ডার অব তারপর ব্রাকেটসের ভেতর যা আছে সেইটা ধরে বলতে হয় যেমন - O(1) হলো ওর্ডার অব ওয়ান এবং O(log n) ওর্ডার অব লগ এন ।

- Constant Time: O(1) -

যখন কোনো প্রোগ্রামে অপারেশন কন্সট্যান্ট টাইম হয় সেই প্রোগ্রামের টাইম কমপ্লিক্সিটি(complexity) ওর্ডার অব ওয়ান O(1)।

ছোট্ট একটি উদাহরণ -

const a = 10;
const b = 5;
const sum = a+b;
const subtract = sum - 10;

উপরের এই প্রোগ্রামে -

1. a ভ্যারিয়েবলে 10 রাখা হয়েছে ।

2. b ভ্যারিয়েবলে 5 রাখা হয়েছে ।

3. sum ভ্যারিয়েবলে (a+b) এর মান রাখা হয়েছে ।

4. subtract ভ্যারিয়েবলে (sum - 10) এর মান রাখা হয়েছে ।

এখানে a ও b ভ্যারিয়েবলের মান যতই রাখা হোক নাহ কেন আমাদের প্রোগ্রামে কিন্তু গাণিতিক অপারেশন মাত্র দুইবারই(২) হবে । অর্থাৎ a ও b ভ্যারিয়েবলের মান যদি ১০০ করে রাখি তবুও গাণিতিক অপারেশন মাত্র দুইবারই(২) হবে । তাই আমরা বলতে পারি এই প্রোগ্রামের টাইম কমপ্লিক্সিটি(complexity) ওর্ডার অব ওয়ান O(1)।

- Linear Time: O(n) -

যখন কোনো প্রোগ্রামে কোনো কাজ একের অধিক বার কোনো ইনপুটের উপর নির্ভর করে হয় সেই প্রোগ্রামের টাইম কমপ্লিক্সিটি(complexity) ওর্ডার অব এন O(n) যাকে Linear Time ও বলা হয়।

যেমন -

let sum = 0;
const summetion = (n) => {
  for (let i = 0; i < n; i++) {
    sum += i;
  }
};
summetion(10);
console.log(sum);

উপরোক্ত প্রোগ্রামে -

1. sum ভ্যারিয়েবলে 0 রাখা হয়েছে।
2. summetion(n) ফাংশন যা n নামে একটি প্যাঁরামিটার নিচ্ছে।
3. এবং ফাংশনের ভেতরে একটি লুপ আছে যা চলবে প্যাঁরামিটার এর মান পর্যন্ত
4. পরের লাইনে sum এর সাথে অ্যাসাইনমেন্ট ও যোগ অপারেশন হচ্ছে।

এখানে যদি n এর মান 100 পাঠানো হয় তাহলে কিন্তু অ্যাসাইনমেন্ট ও যোগ অপারেশন 100 বারই হবে সাথে sum এর মানও বাড়তে থাকবে । আর যদি n এর মান 1 হতো তাহলে একবারই অপারেশন গুলো হতো । এখন আমরা খুব সহজেই বলতে পারি যে, এই প্রোগ্রামের টাইম কমপ্লিক্সিটি(complexity) ওর্ডার অব এন O(n) ।

- শেষের কথা - বিগ ও নোটেশন (Big O) নিয়ে আজ এ পর্যন্তই এই ব্লগের মূল উদ্দেশ্য ছিলো সহজ একটা ইন্ট্রোডাকশন। কোড নিয়ে যখন আরও উদাহরণ দেখবেন তখন এটি সম্পর্কে ভালো আইডিয়া চলে আসবে, যা আমার টাইম এবং স্পেস কমপ্লিক্সিটির (complexity) ব্লগে থাকবে।

আমরা ভূল করবো এবং তা সমাধানও করবো বা চেষ্টা করবো । তাই যদি কোনো সন্দেহ থাকে তাহলে প্লিজ আমাকে জানাতে ভূলবেন নাহ । আমরা শিখতে চাই সেইটা ভুল থেকে হলেও। শাকিল বাবু

ধন্যবাদ সবাইকে ।

For more articles visit here.