গত পর্বগুলোতে আমি সিলেকশন সর্ট(Selection sort) এবং বাবল সর্ট(Bubble sort) অ্যালগরিদম নিয়ে আলোচনা করেছিলাম এই পর্বে আরও একটি সহজ সর্টিং অ্যালগরিদম নিয়ে আলোচনা করবো নাম ইনসার্শন সর্ট(Insertion sort) ।
ইনসার্শন সর্ট(Insertion sort) অ্যালগরিদম :-
এই সর্টিং অ্যালগরিদমের মূল বিষয় হলো - একটি নির্দিষ্ট সংখ্যার জন্য এমন একটি জায়গা খুঁজে বের করা যেখানে সংখ্যাটিকে রাখলে তার আগের সংখ্যাটি তার থেকে ছোট বা সমান হবে এবং পরের সংখ্যাটি তার থেকে বড় হবে । তবে সংখ্যাটি যদি অ্যাঁরে বা লিস্টের সবচেয়ে ছোট বা বড় সংখ্যা হয় তাহলে তার জন্য সবার প্রথমে জায়গা করে দিতে হবে ।
ধরি, আমাদের কাছে [10,30,40] এই অ্যাঁরেটি ছোট থেকে বড় ক্রমে সাজানো আছে । আমি এই অ্যাঁরেতে আরেকটি সংখ্যা যুক্ত করতে চাই সংখ্যাটি হলো 20 । এখন আমাকে 20 কে এমন এক জায়গায় বসাতে হবে যেখানে তার আগের সংখ্যা তার থেকে ছোট বা সমান হবে এবং তার পরের সংখ্যাটি তার থেকে বড় হবে ।
যদি অ্যাঁরেতে লক্ষ করি তাহলে দেখতে পারবো যে, সেই কাঙ্খিত জায়গাটি হচ্ছে <mar>10</mark> এর পরের অবস্থান কারণ, 20 থেকে 10 ছোট এবং 30 বড় । এখন যেহেতু 10 এর পরের অবস্থানে 30 আছে, তাহলে 30 এর জায়গায় 20 কে বসাতে হলে অ্যাঁরের শেষ থেকে অর্থাৎ 40 কে এক ঘর ডানে সরাতে হবে এখন 40 যেখানে ছিলো সেই ঘরটি কিন্তু ফাকা -
<mark>[10, 30, _, 40]</mark>
এরপর 30 কে এক ঘর ডানে সরাই - <mark>[10, _, 30, 40]</mark>
এখন ফাকা জায়গাটি কিন্তু 20 এর জন্য পারফেক্ট জায়গা অর্থাৎ, যে স্থানটি ফাকা তার আগের সংখ্যাটি 20 থেকে ছোট এবং পরের সংখ্যাটি 20 থেকে বড় । তাহলে ফাকা জায়গাটিতে 20 কে এসাইন করি -
<mark>[10, 20, 30, 40]</mark>
এতক্ষণ যে পদ্ধতিতে একটি সংখ্যা অ্যাঁরেতে সাজানো হলো এই পদ্ধতিকেই আমরা ইনসারশন সর্ট(Insertion sort) বলতে পারি ।
অ্যারে(Array) ও ইনসার্শন সর্ট(Insertion sort) -
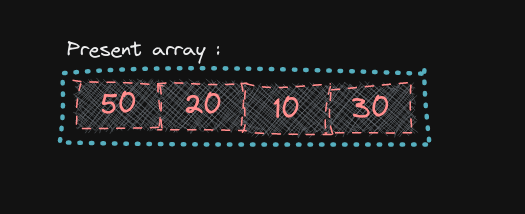
তো চলুন এখন একটি এলোমেলো অ্যাঁরে বা লিস্টকে ইনসারশন সর্ট(Insertion sort) পদ্ধতিতে ছোট থেকে বড় ক্রমে বা Accending order এ সাজাই । ধরি, আমার কাছে একটি অ্যারে আছে -
[50, 20, 10, 30]
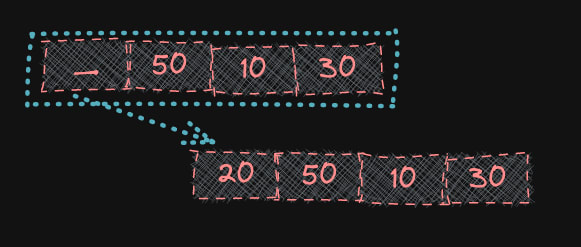
স্টেপ(০১) :- প্রথমে 50 এবং 20 এর মধ্যে ছোট সংখ্যার জন্য উপযুক্ত জায়গা খুঁজে বের করবো । এক্ষেত্রে, 20 কে 50 এর অবস্থানে বসাতে হবে তাই 50 কে এক ঘর ডানদিকে সরাই । এখন কিন্তু 50 এর জায়গা খালি তাই খালি জায়গায় 20 কে এসাইন করি -
[20, 50, 10, 30]
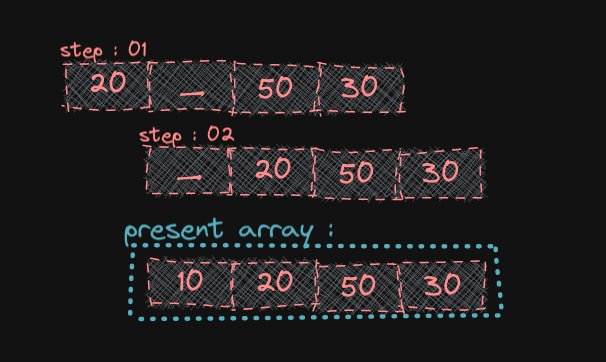
স্টেপ(০২) :- 50 এবং 10 এর মধ্যে 10 এর জন্য উপযুক্ত জায়গা খুঁজে বের করি । এক্ষেত্রে, অ্যারের প্রথমে 10 কে রাখতে হবে অর্থাৎ 20 এর অবস্থানে । তাই, প্রথমে 50 কে এক ঘর ডান দিকে সরাই - <mark>[20, _, 50, 30]</mark>
এখনও উক্ত ফাকা স্থানটি কিন্তু 10 এর উপযুক্ত জায়গা না তাই 20 কেও এক ঘর ডান দিকে সরাই - <mark>[_, 20, 50, 30]</mark> এখন ফাকা স্থানে অর্থাৎ 20 এর আগের ঘরে 10 এসাইন করি -
[10, 20, 50, 30]
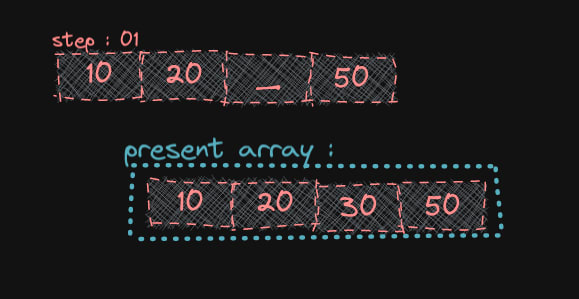
স্টেপ(০৩) :- 50 এবং 30 এর মধ্যে 30 এর জন্য উপযুক্ত জায়গা খুঁজে বের করি এক্ষেত্রে, 20 এবং 50 এর মাঝে । তাই 50 কে এক ঘর ডানদিকে সরাই -
<mark>[10, 20, _, 50]</mark> এখন ফাকা জায়গাটিতে 30 কে এসাইন করি -
[10, 20, 30, 50]
ব্যাস, উপরোক্ত অ্যারে বা লিস্টটি ছোট থেকে বড় ক্রমে অর্থাৎ Accending order এ সাজানো হয়ে গেলো । এখন আপনি যদি বুঝতে না পারেন তাহলে খাতা-কলম নিয়ে বিষয়টি বোঝার চেষ্টা করতে পারেন । যদি প্রথম বা দ্বিতীয় বারে বিষয়টি বুঝে থাকেন তাহলে আপনি একটি বড় অ্যারে বা লিস্টকে খাতা-কলমে সর্ট করতে পারেন । তো চলুন এখন ইমপ্লিমেন্টেশন করা যাক -
In Python :
def insertionSort(arr):
for i in range(1, len(arr)):
# arr[i] কে currentValue তে এসাইন করি
currentValue = arr[i]
# currentValue এর জন্য উপযুক্ত স্থান খুঁজে বের করি
j = i - 1
# যদি j, 0 থেকে সমান বা বড় হয় এবং arr[j] থেকে currentValue ছোট হয়
while j >= 0 and arr[j] > currentValue:
# arr[j] কে তার পরের ঘরে রেখে দিই
arr[j+1] = arr[j]
# j এর মান 1 করে কমাই
j -= 1
# এখন খালি জায়গায় currentValue কে বসাই
arr[j+1] = currentValue
return arr
In JavaScript :
function insertionSort(arr) {
// একটি currentValue নামে ভেরিয়েবল নিই
var currentValue;
// i এর মান 1 থেকে len(arr) এর আগ পর্যন্ত 1 করে বাড়াই
for (var i = 1; i < arr.length; i++) {
// arr[i] কে currentValue তে এসাইন করি
currentValue = arr[i];
// currentValue এর জন্য উপযুক্ত স্থান খুঁজে বের করি (j = i - 1)
// যদি j, 0 থেকে সমান বা বড় হয় এবং arr[j] থেকে currentValue ছোট হয়
for (var j = i - 1; j >= 0 && arr[j] > currentValue; j--) {
// arr[j] কে তার পরের ঘরে রেখে দিই
arr[j + 1] = arr[j];
}
// এখন খালি জায়গায় currentValue কে বসাই
arr[j + 1] = currentValue;
}
return arr;
}
আপনি চাইলে জাভাস্ক্রিপ্ট কোডে for লুপের পরিবর্তে while লুপ ব্যাবহার করতে পারেন ।
উপরোক্ত কোড বিশ্লেষণ :-
উপরের প্রোগ্রামে, প্রথমে i=1 থেকে অ্যারের লেন্থ পর্যন্ত লুপ চালিয়েছি । তারপর currentValue নামে একটি ভেরিয়েবলের মাঝে অ্যারের Present ভ্যালুকে রাখছি । এক্ষেত্রে কারেন্ট ভ্যালুটি যাতে হারিয়ে না যায় তা নিশ্চিত করছি কারণ পরবর্তীতে এই currentValue কেই তার যথাযথ স্থানে রাখতে হবে ।
তারপর ভেতরের লুপে j >= 0 এবং arr[j] > currentValue এইভাবে চেক করতেছি । এখানে, যদি j এর মান 0 থেকে ছোট হয় তাহলে আমি বুঝতে পারবো যে অ্যারে বা লিস্টের সব উপাদানই currentValue থেকে বড় । আবার, j এর মান যদি 0 থেকে বড় বা সমান হয় তাহলে দ্বিতীয় শর্তপরীক্ষা করা করবো অর্থাৎ arr[j] > currentValue ।
এখন যদি দ্বিতীয় শর্ত অর্থাৎ arr[j] > currentValue সত্য হয় তাহলে, arr[j] কে আমরা এক ঘর ডানে সরিয়ে দিব - arr[j + 1] = arr[j]
আবার, arr[j] > currentValue যদি মিথ্যা হয় তাহলে, লুপ থেকে বের হয়ে arr[j + 1] এ currentVal কে এসাইন করে দিব - arr[j + 1] = currentVal ইত্যাদি ।
যেকোনো অ্যালগরিদম বাঁ ডাটা-স্ট্রাকচারের মূল কনসেপ্ট যদি আপনি ভালোভাবে বুঝতে পারেন তাহলে যেকোনো প্রোগ্রামিং ল্যাঙ্গুয়েজ ব্যাবহার করেই ইমপ্লিমেন্ট করতে পারবেন । চলুন ইনসার্শন সর্ট(Insertion sort) অ্যালগরিদমের টাইম ও স্পেস কমপ্লেক্সিটি বের করা যাক -
টাইম কমপ্লেক্সিটি(Time Complexity) :
উপরোক্ত কোড লক্ষ করলে আশা করি টাইম কমপ্লেক্সিটি(Time Complexity) বলে দিতে পারবেন । এই অ্যালগোরিদমেরও টাইম কমপ্লেক্সিটি(Time Complexity) O(n<sup>2</sup>) ।
স্পেস কমপ্লেক্সিটি(Space Complexity) :
উপরের প্রোগ্রামে একটু খেয়াল করলে দেখতে পারবো যে, প্রোগ্রামে একটি লিস্ট বা অ্যারে প্যারামিটার হিসেবে নেওয়া হয়েছে । এবং যা কাজ-কারবার করা হয়েছে তা এই অ্যারে বা লিস্টের মধ্যেই । এই অ্যারে বা লিস্টে কিন্তু কোনো নতুন উপাদান সংযোজন, বিয়োজন ইত্যাদি কিছুই করা হয় নাই । তাহলে বলতে পারি অ্যারে বা লিস্টটি Constant । এখন আপনার কাছে আমার প্রশ্ন এই প্রোগ্রামের স্পেস কমপ্লেক্সিটি(Space Complexity) কত ?
<mark>আশা করি পেরেছেন হ্যাঁ স্পেস কমপ্লেক্সিটি(Space Complexity) হচ্ছে - O(1) । </mark>
ব্রাভো, যদি এতদূর পর্যন্ত আপনি ঠিকঠাক ভাবে পড়ে থাকেন তাহলে আমি ধরে নিতেই পারি ইনসার্শন সর্ট(Insertion sort) অ্যালগরিদম সম্পর্কে ভালো একটা দখল চলে আসছে ।
যদি সত্যি বুঝে থাকেন তাহলে একটি কাজ করতে পারেন, উপরোক্ত অ্যারেটিকে আমি কিন্তু Accending Order অর্থাৎ ছোট থেকে বড় ক্রমে সাজিয়েছি এখন আপনি ইনসার্শন সর্ট(Insertion sort) অ্যালগরিদম ব্যাবহার করে অ্যারেটিকে Decending Order অর্থাৎ বড় থেকে ছোট ক্রমে সাজানোর চেষ্টা করবেন । খুবই সহজ একটি কাজ আশা করি পারবেন শুভকামনা রইলো ।